Games of Chance

In the earliest laboratory notebooks, the wall-mounted m­echanism shown in this image was simply called “the pinball machine.” In the published output of the research program of which it was a part, it wen­t by the more dignified­ appellation Random Mechanical Cascade, yielding a catchy acronym: RMC. Around the lab, however, the ­device was known affectionately as ­Murphy, since if anything could go wrong, it would.­

­In a way, of course, this was exactly the point: the whole system—the nine thousand polystyrene balls droppin­­g through a pegboard of 330 precisely cantilevered nylon pins, the real-time photoelectric counters tallying (by LED readout) the segmented heaps forming belo­w, the perennially balky bucket-conveyor for resetting an experimental run—had all been painstakingly constructed and ca­librated in order first to exemplify, and then to defy, what the Victorian statistician ­Francis Galton dubbed the “Law of Frequency of Error.“

­By this, the old mutton-chopped eugenicist meant something a good deal more than that cozy proverb concerning the minor irritations of the world. Indeed, Galton believed he was tugging at the toga of Jove:

Order in Apparent Chao­s. I know of scarcely anyt­hing so apt to impress the imagination as the wonderful form of cosmic order expressed by the “Law of Frequency of Error.” The law would have been personified by the Greeks and deified, if t­hey had known of it. It reigns with serenity and in complete self-effacement amidst the wildest confusion. The huger the mob, and the greater the apparent anarchy, the more perfect is its sway. It is the supreme law of Unreason.^[1]

A law, therefore, most devoutly to be desired. But what was it? The law of the normal. More on this in a moment.

• • •

First, the prehistory of the RMC and the investigations that gathered around it. Scene: the men’s room of a dormitory on the campus of American University in Washington, DC, in the second week of August 1977. An older man wearing a raincoat as a bathrobe (who packs a bathrobe to attend an academic conference?) shaves his lathered face in the mirror while conversing with a distinguished physicist. The shaving man says something along the lines of, “How can I put a kid in a fighter plane and send him into a combat situation unless I’ve done absolutely everything I can to make sure that every mechanical and electrical system on his aircraft is going to behave?” The physicist, who is an expert on plasma propulsion with decades of experience in aeronautical engineering, agrees. One can’t be too careful; one has to test for every possibility.

And because the man who is shaving is James S. McDonnell, the long-time head of the most powerful avionics corporation in the world (McDonnell-Douglas), and because the physicist is Robert G. Jahn, the dean of the School of Engineering at Princeton University, their conversation will, shortly thereafter, shape up as a research program (based at Princeton, substantially funded by McDonnell)—a program to investigate the sensitivity of a variety of micro- and macro-mechanisms under changing local and non-local conditions. Reasonable enough. But because these gentlemen were in Washington that summer to attend the annual meeting of the Parapsychological Association, they were after a little more than garden-variety aerospace stress testing. What they really wanted to know was what the machines knew. Cue the soundtrack from The Twilight Zone…

Actually, don’t. In fact, forget about spoon bending. Forget New Age spirituality. Forget metaphysics altogether, along with what you think you know about the crystal-worshipping enthusiasts of matters paranormal. Go back instead to the world of Eisenhower-era military-industrial research, for that is the world out of which both these men came, and the world to which they still, in the mid-1970s, basically belonged: the world of right-stuff aviators and pocket protectors, the world of jets and the tow-headed warriors who made them fly. Men who hurtle through the air several miles above the earth at the speed of sound are more than ordinarily dependent on the smooth functioning of technology; it is a vulnerability that tends to encourage the fetishizing of the machines that bear them aloft, together with a kind of nervous, animistic intimacy not entirely characteristic of a mechanico-materialist worldview. Which is to say, airmen across the twentieth century—and airmen exposed to the white-knuckle exigencies of combat above all—have consistently talked to their aircraft, named them, reasoned with them, cajoled and cursed them, stroked and indulged them. And within these competitive and fatalistic fraternities, where being lucky was tacitly understood to be every bit as important as being skilled, systematic differences were readily observed between operators, some of whom could get their spooky machines to do the seemingly impossible again and again, while others, regardless of the assiduous labors of ground crews, appeared consistently to bring out the worst in their gremlin-prone equipment. Some pilots, it seemed, could sweet-talk their terrible birds; others were forever in the weeds.

All this was anecdotal, of course—the hangar chat of cocksure youths who made their living dealing and defying death. The empirical basis for such superstitious distinctions presumably lay in (subtle) operator errors, (subtle) operator capacities, and the (pervasive) vagaries of naked chance. But dismissing the widely held and deeply felt intuitions of communities of highly trained experts is always a dangerous game, and in the 1960s, a decade that saw the rise of cybernetics and new research emphasis on human-machine interfaces, there were those who began to ask whether the private and semi-private voodoo of the pilots might represent something more than merely the fetching folkways of a peculiar tribe. What if these men talked to their planes because their planes were listening? Could those staggeringly complex and jumpy supersonic jetfighters—in several respects the most sophisticated pieces of technology ever realized by human beings—conceivably “sense” their operators? Feel their terror or confidence? Did the machines somehow respond to their masters in ways that transcended the fly-by-wire link between the brain, the hand, and the ailerons? Today, perhaps, this seems mostly like a question for late-night television. Forty years ago, however, it was the sort of question that could interest a defense contractor.

Indeed, Jahn’s own interest in testing for evidence of such “anomalous” interactions between mind and machine stemmed from his efforts to replicate experimental work done in the late 1960s by a fellow plasma physicist, the German Helmut Schmidt, then employed as a research scientist at Boeing.^[2] Schmidt appeared to have demonstrated that a particular experimental subject had the capacity to guess numbers generated by a randomizing algorithm at a rate considerably outside the calculated margins of probability. Working with an interested undergraduate student in the mid-1970s, Jahn had successfully reproduced some similarly anomalous statistical results using a random number generator of his own devising, and by the time he found himself chatting with McDonnell in the summer of 1977, Jahn was already contemplating turning his research attentions fully to the sustained investigation of what he would call “the role of consciousness in the physical world.” He would give the next thirty years of his life to this work, building the controversial PEAR (Princeton Engineering Anomalies Research) laboratories in the basement of the engineering building at Princeton University (in the teeth of lively opposition), and generating, with his co-author and collaborator Brenda Dunne (whom he encountered for the first time at that same 1977 conference), a massive database of tens of millions of experimental trials in which human subjects sought to influence the workings of various devices merely by thinking, wishing, visualizing, or praying. Together, Jahn and Dunne (who closed the original PEAR lab in 2007, but continue to write and speak about their work) claim to have demonstrated that human cognition has a real and measurable, if small, influence on the perceivable dynamics of the material world. If they are correct, the implications for physics, religion, etc., are enormous. If they are not correct, their labor-intensive and largely sober efforts over three decades limn a zone of techno-scientific quixotism perhaps best thought of as a suburb of performance art. Let us go forward as if we have not decided.

• • •

The idea for the Random Mechanical Cascade itself can be traced to the heady early days of Jahn’s encounter with Dunne, then a graduate student in psychology at the University of Chicago working on self-perception and the quantitative analysis of subjectivity. On a visit together to the city’s Museum of Science and Industry in 1978, Jahn and Dunne stood for a time in front of a large pachinko-like exhibit designed to exemplify what mathematicians call the “normal” or “Gaussian” distribution, a curve fundamental to the study of probability and to the statistical investigation of many phenomena.

A mathematical excursus will hopefully be forgiven. The formula for this important curve is the ugly-looking

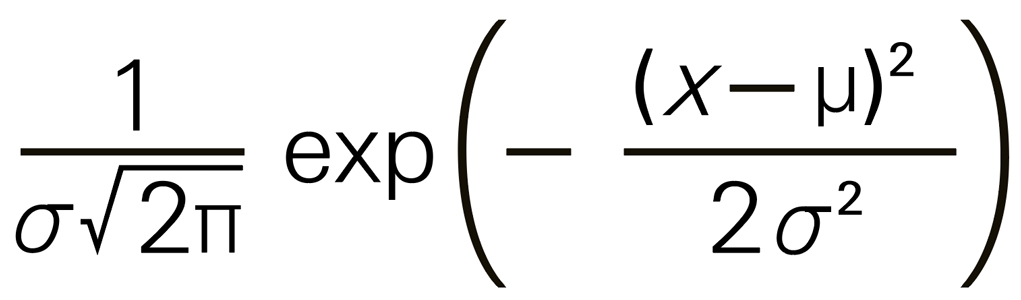
­but a word-probl­em description of the thing is a little less forbidding. Imagine flipping a coin, say, a hundred times, and writing down the number of heads; now imagine repeating that exercise ten thousand times; you have ten thousand numbers in front of you, all of which are between zero and one hundred. It stands to reason that you will very, very rarely have flipped a hundred heads in a row, and, conversely, you will have mighty few streaks of a hundred tails; the majority of your trials will have netted—assuming you are using an unshaved coin and that the gods are staying out of the affair—in the neighborhood of fifty heads and fi­fty tails. In fact, if you were to plot your totals from “no heads at all” over to “all ­heads,” the resulting graph would (in all likelihood—though, to be sure, anything is possible) end up looking like that familiar thing called a “bell curve.” Your graph is a good approximat­ion of the normal. The more iterations of a hundred flips you do, the closer you’ll get to the actual normal (though your approximation will never be perfect, bec­ause it will al­ways be a stepwise and bounded function, since your data is falling out in discrete integer values between zero and one hundred; the true normal curve is smooth and continuous).

For reasons that are a little tricky to explain, a great deal of the stuff in the universe can be characterized using this curve. For example: if I measure the length of Manhattan many times using a ruler, I will come up with a mess of slightly different values; plotted, they will distribute themselves in one of these normal curves (with the odds being that my best answer will lie at the mean). Similarly, if I make everyone in Manhattan take an IQ test, their results, too, will fall out in a normal distribution. Ditto a host of other traits of this population, and, moreover, of all the other populations on the island, from the roaches to the seagulls. At first glance, there is no particular reason why this should be, and, depending on your appetite for mathematics, error theory, and/or population biology, you may already understand why this happens, or get curious enough to try to figure it out, or already be reading another article.

Be that as it may, Francis Galton, as we have seen, was obsessed with this recurring pattern—for this was his “Law of the Frequency of Error”—and saw in it nothing less than a kind of cosmic order of disorder. If he had been a man inclined to religiosity (as he emphatically was not), he might have placed the curve at the devotional center of his life. Instead, he used it to prove to his own satisfaction that all re­ligion was bunk—which he did by plotting the longevity of those much prayed-for (particularly English sovereigns, since “God save the Queen/King” was a constant refrain of the inhabitants of the British Isles) against everyone else. He found no statistically significant difference.^[3]

A curve that could help disprove the existence of God was a curve the vigorously anticlerical Galton wanted to preach about, and as an aid in his proselytizing efforts he commissioned the London instrument makers Tisley & Spiller to build for him a clever demonstration device of his own design, now known as a Galton Board.^[4] The operation is simple: a reservoir of little balls empties down through a funnel-like feeder into a pyramidal array of pins; having cascaded through this forest, the balls stack up in a set of vertical ch­annels at the bottom of the glass-fr­onted box. Bec­ause of the particular configuration of the pins—which are arranged in what is known as a quincunx, the pattern used in orchards to give each tree maximum space by of­fsetting the rows—the balls in such a contraption fall out in the vertical columns in a distribution that approaches the normal. In fact, the whole system is an exact analogue of that coin toss exercise, since at each row of the board a falling ball hits a pin ­and has a—theoretically equal—chance of going right or left. For a ball to end up all the way at the extreme right at the bottom of the board it must have gone right every time it hit a pin—the equivalent of flipping a perfect streak of heads. What generally happens is that balls go left sometimes and right sometimes and thus end up in the middle channels at the bottom; the line traced by the tops of all the stacks of balls should be—if you have the thing on an even surface, if the pins are all in place, if the rules of chance are working as they ought—a good approximation of the normal curve.

Should be. Which brings us back to Jahn and young Brenda Dunne at the Museum of Science and Industry in the autumn of 1978, where a la­rge wall-mounted Galton Board churned away for a class of schoolchildren, whose teacher, back to the device, was holding forth about the glories of binomials and the magnificent pervasiveness of the normal distribution. But as she did so, Dunne and Jahn, enthrall­ed by a playfully malevolent sense of the possible, set their minds to defying the odds. And, as luck (or something else) would have it, no sooner did they be­gin their uncontrolled experiment in tilting the distribution to the right by force of will, than the little hillock forming at the bottom of the machine began to drift markedly to the right—unbeknownst to the lecturer, but to the increasing hilarity of her students.

Jahn hired Dunne. And back in Princeton, with McDonnell’s backing, they set to the task of building a Galton Board of sufficient precision to test rigorously whether the mind could affect the workings of the world.

• • •

This proved more difficult than it might seem. A perfect disorder—a genuinely consistent stochasticity—must be coaxed from the world and tended with some care, since this fallen universe displays myriad disorienting tendencies toward patterned regularity. The cascading balls of the early versions of the RMC did not tumble with the looked-for indifference: they generated, for instance, static electricity, which in accumulating distorted their dynamics and wreaked havoc on the sensitive counters that were supposed to tally the final segmented distributions. Moreover, a good-looking normal distribution turned out to require a surprising amount of jury-rigging, given the ostensible cosmic ubiquity of the curve itself. If the pins themselves were too rigid, or the balls too bouncy, the final distributions could be almost perfectly flat, or even, depending on the configuration, peculiarly bimodal (double-humped like a dromedary). In the end, it took the better part of a year (and something close to $100,000) to realize the handsome device that adorned the wall of the PEAR laboratory for some twenty years, and that clattered through more than ten thousand cycles under the watchful eye of hundreds of experimenters who sat on the plush couch before it and thought “go right” or “go left” for hours on end. The total tally and final configuration of each run (a full cycle took about fifteen minutes) were meticulously recorded in dozens of laboratory notebooks, which amount to the archival residue of the most sustained effort ever undertaken to test whether, in fact, faith can move a mountain—a small, controlled mountain of polystyrene balls.

The answer, it would seem, is maybe. But probably only a very little bit. Jahn and Dunne observed that deviations from the RMC’s normal distribution corresponded with the conscious intentions of its operators much more often than one would have expected in a world of perfectly ordered disorder; though, strangely, the effect was a good deal more pronounced when people tried to get the balls to go left.^[5]

• • •

In her recent study of the place of the test in the Western metaphysical and anti-metaphysical traditions, Avital Ronell pauses on a cryptic passage in Nietzsche’s Gay Science:

We should leave the gods in peace … and rest content with the supposition that our own practical and theoretical skill in interpreting and arranging events has now reached its apogee. But at the same time, we must not conceive too high an opinion of this dexterity of our wisdom, since at times we are positively shocked by the wonderful harmony that emerges from our instruments—a harmony that sounds too good for us to dare claim the credit for ourselves. Indeed, now and then someone plays with us—good old chance.^[6]

For Ronell, concerned with the ways that the techno-scientific obsession with testing has driven a wedge between how to live and how to know, these lines show Nietzsche—the high prophet of a true life-science he can but dimly descry—carefully removing the finger-grip of Providence from the throat of amor fati, the love of fate. What matters most, as Ronell puts it, “cannot be proven once and for all,” but rather, as Nietzsche himself explains, must be “proven again and again.”

What lingers is that lovely phrase “spielt einer mit uns”—someone plays with us. As if the empirical investigation of reality were a kind of four-handed exercise. It is a tempting notion. Chance plays with us, to be sure, but perhaps we can play along. This would suggest that every test is first and foremost a game we have forgotten how to play. And this may be the answer: a means by which to protect ourselves, and perhaps even the gods, from the seductive devastation of what Ronell calls the test drive.

But is such wistful Spiellust quite warranted? Does the scene want our pity? After all, perhaps—yes, per-haps—our young and vigorously casual scientist of the paranormal was at that very moment playing along.

And where is Murphy now? At the offices of a financial services company in Southern California! [video no longer available to the public—Eds.]