Fall 2012

Coming Full Circle

The Traveling Salesman Problem and the dream of optimality

D. Graham Burnett

The problem is easily stated: given a finite number of points, find the shortest connecting path—the shortest line that touches each point once, and closes on itself by returning to the point of departure. What could be more straightforward? It is a problem a child can understand—a simple game of connect-the-dots.

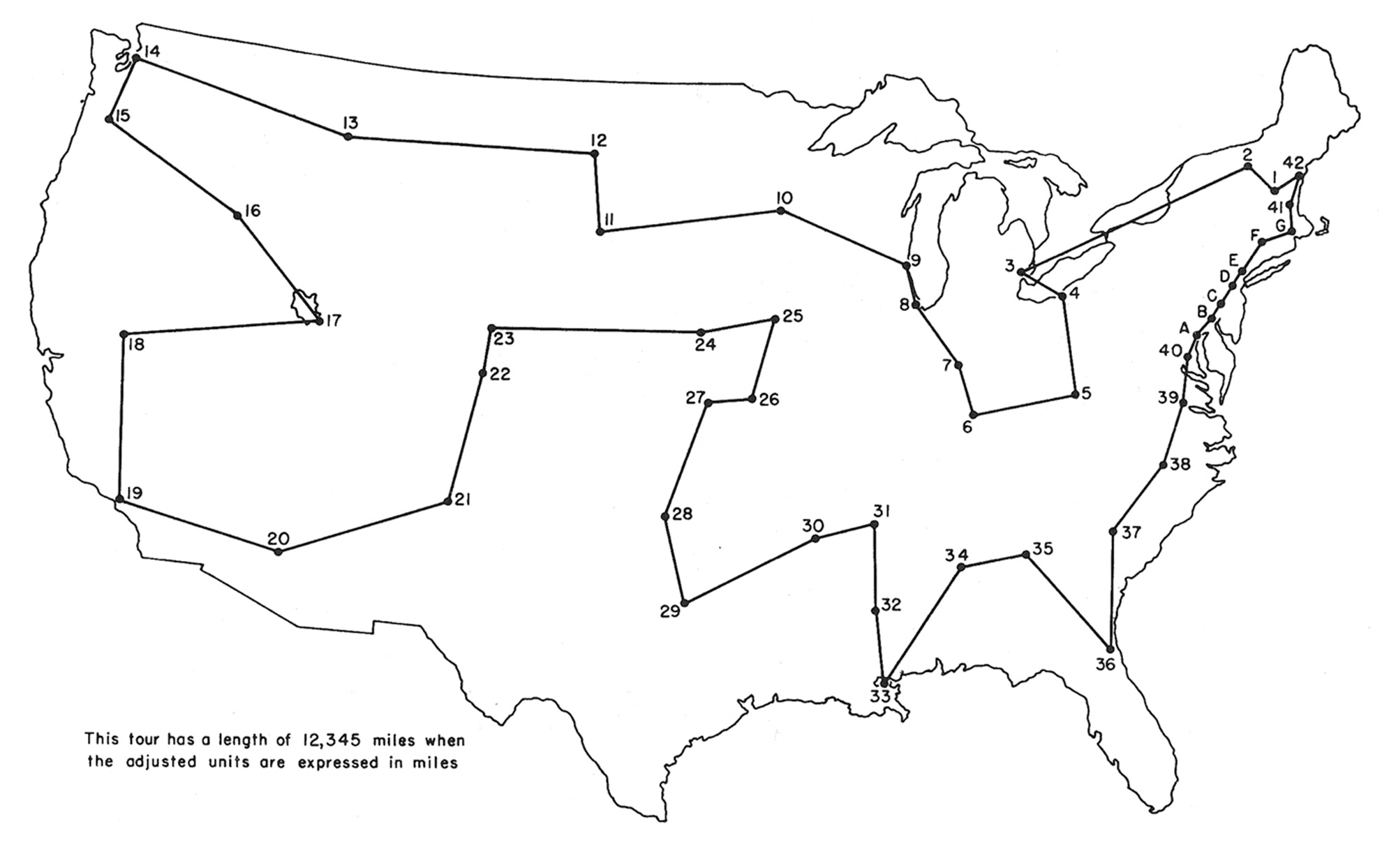
It is also, however, a problem of absolutely legendary difficulty. Add more than a handful of points, and a brute-force solution requires more computer-years than there are particles in the universe. Untold millions of human- and machine-hours have now been expended on the problem, which has come to function as a touchstone for theories of complexity, and as a kind of conceptual fetish object at the center of the overlapping disciplines of applied mathematics, algorithm theory, and computational geometry. There is, at present, a million-dollar bounty on its head, and some of the very deepest questions in theoretical computer science hang on the prospect of a general solution.^[1]

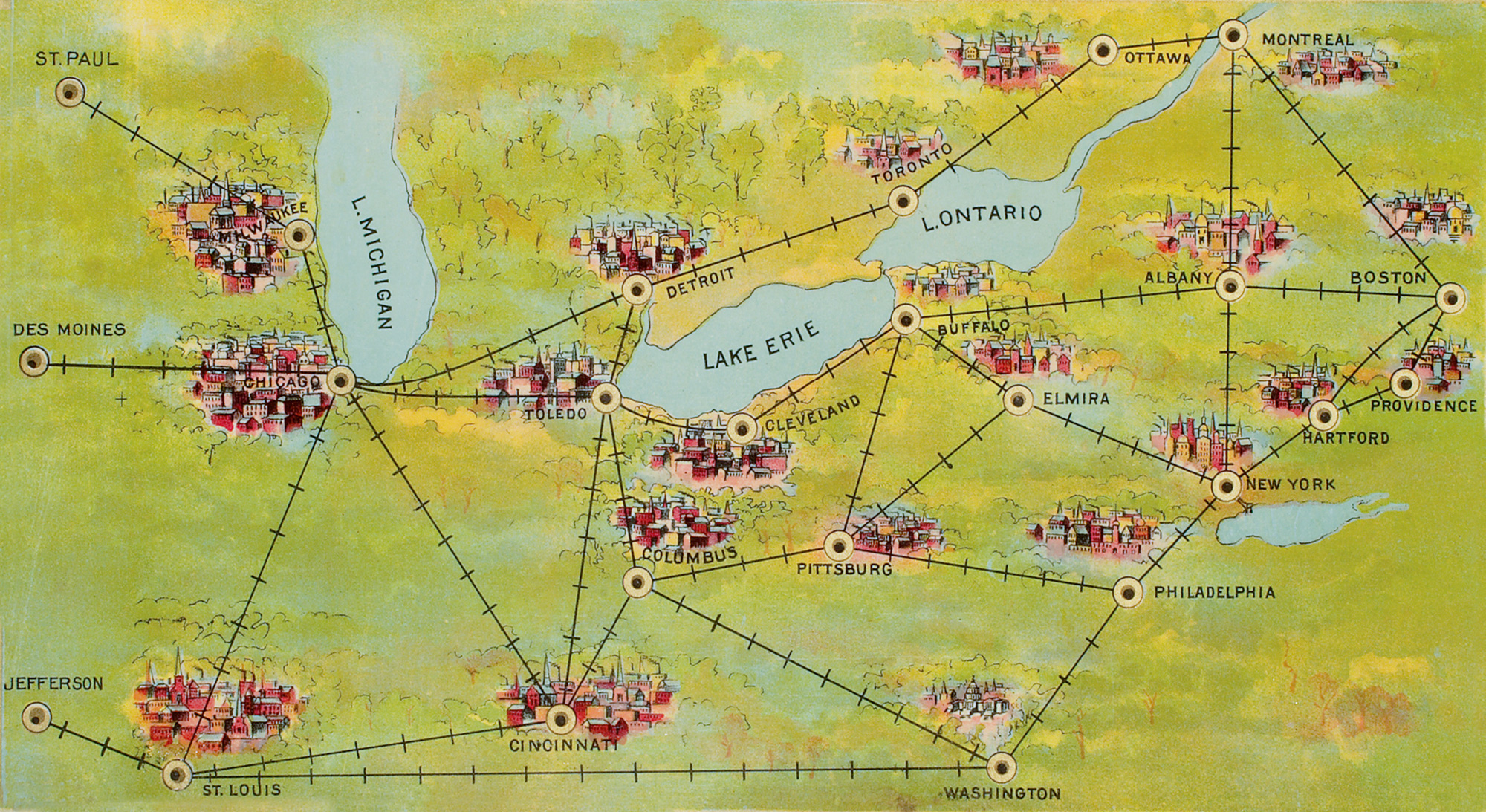
Mathematicians call it the TSP—the Traveling Salesman Problem, a moniker that speaks subtly to the twinned genealogies of capitalism and calculating rationality. And indeed the problem—which has become nothing less than a model system for understanding what can be understood—began its life as a head-scratcher for the shock troops of consumer economics, those late eighteenth- and early nineteenth-century itinerant missionaries of an increasingly abstract and globalizing market. Those men girded their loins and shouldered their sample cases only after perusing the new cartographies made available by centralizing states and expanding empires. They plotted their routes, these drummers, and did so with an eye on the bottom line. Which is to say, actual travelling salesmen fretted the TSP long before a clutch of Cold War theoreticians at the RAND Corporation found their way to it, and restyled it as an all-purpose test of number-crunching power and analytic ingenuity. Tellingly, the earliest formulation of the problem would seem to hail from a German-language gazetteer/handbook prepared in the early 1830s for commercial travelers intending to make tours through the Swiss cantons and the German lands. That volume (Der Handlungsreisende—von einem alten Commis-Voyageur), mindful that time and space were money, carefully laid out a thirty-three-city circuit—Freiberg-Dresden-Leipzig-Halle, etc.—that pretended to optimality.^[2]

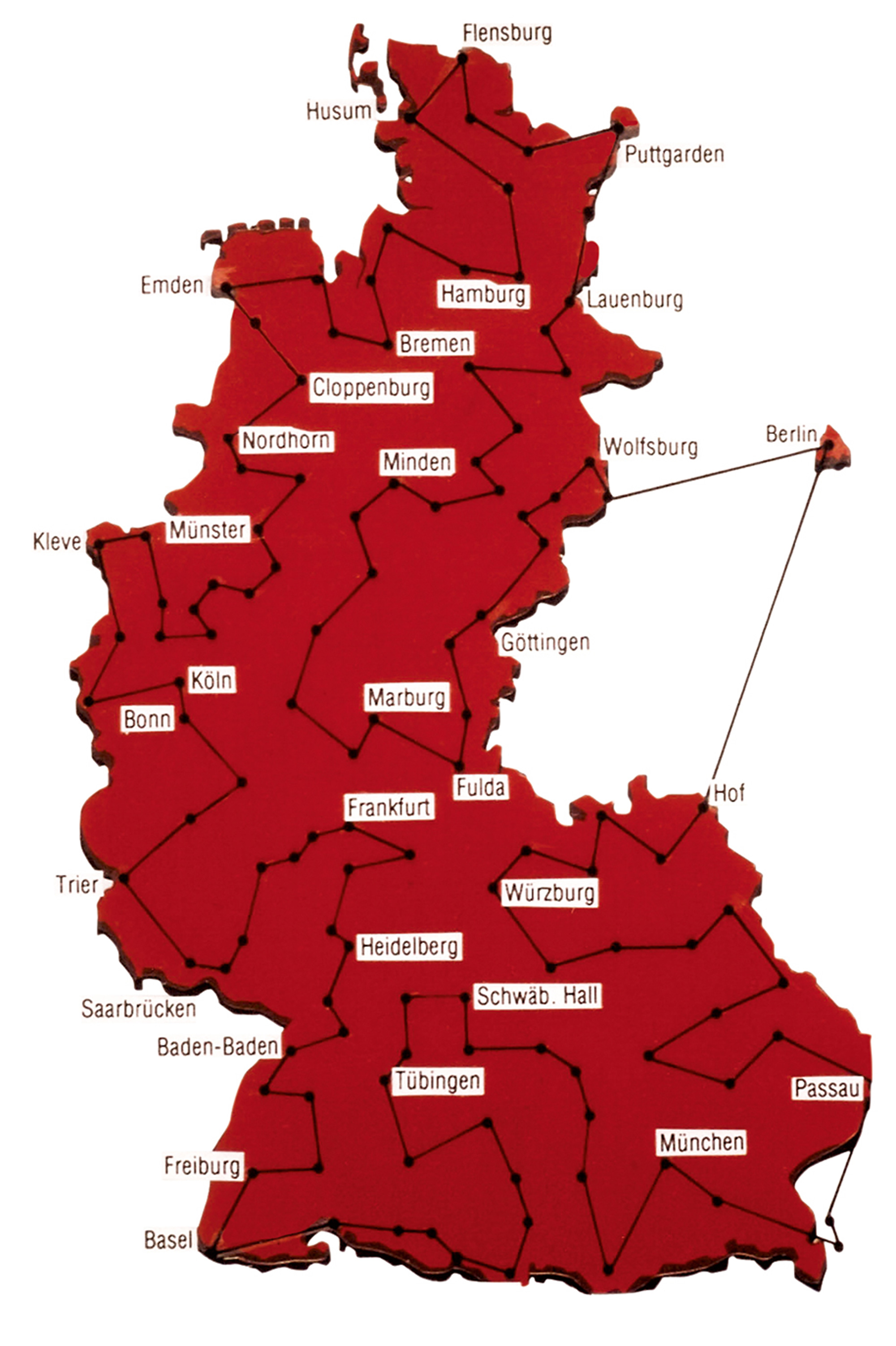
Optimality. Life itself is obviously not an optimization function. Nevertheless, one could do worse than describe modernity as the ideological commitment to a progressive extension of optimization logic to domains of self and society not previously understood to yield to such treatment. Where the limits of this exercise lie remains unclear. Again and again it has proven possible (and profitable) to step over the various boundaries inscribed by tradition, habit, and custom. By these lights, “logistics”—the formal science of spatio-temporal optimization; the toolkit for synchronized coordination of human beings and materials in dynamic systems; the study of all problems that can be stated in the form, “Who and what are where when, and how could we do it better?”—must be understood as nothing less than the standard-bearer for social, political, and economic transformation across the last two centuries. Where the formal concepts and technics of logistics have gone—and they have sequenced impressively through war, wealth production, and governance—the modern world has followed.

It is difficult to résumé this history succinctly. And perhaps quixotic to attempt to do so in pictures. But given this ambition, there is much to be said for a survey of graphical representations of the TSP. The trajectory of such a sequence—from the scratch pad plottings of proto-capitalist peddlers to the meta-analytic musings of those who hope to solve the general problem of what problems can be solved—traces an efficient (or is it scenic?) route across the fields of metaphorical money and countinghouse metaphysics.

Let’s take the tour.

By the late nineteenth century, the traveling salesman had become a significant figure in the cultural imagination. The basic problem of his life—an optimized tour of target towns—was sufficiently familiar and pressing to serve as the basis of a popular American board game. No general mathematical formulation of the TSP was available at the time, although several related problems (Leonhard Euler’s Bridges of Königsberg solution; William Hamilton’s Icosian) had laid the analytical groundwork for what would become the twentieth-century solution efforts. Image courtesy Pamela Laird.

By the 1920s, the TSP was a sufficiently pressing problem for large companies that secretarial training could include instruction on route-optimization, and map cabinets with pin and string kits for circuit planning were available for office use. Such practical applications required thinking about real roads and actual overland distances (later, most mathematical versions of the problem optimized purely geometrical, straight-line paths). Image from Secretarial Studies, 1922. Courtesy William Cook.

The earliest inquiry into the TSP by a research mathematician appears to have been made around 1930 by Karl Meneger, a member of the Vienna Circle. It is possible that he conveyed his enthusiasm to Hassler Whitney, then at Princeton, during a mutual visit to Harvard in 1930 or 1931. Merrill Flood, who brought the problem with him when he went to work at RAND in California, claimed to have been introduced to it by Whitney. It was at RAND that George Dantzig—a key figure in the history of both linear programming and operations research—succeeded in making a major TSP breakthrough. Using techniques he had honed doing quartermaster logistics for the Navy during World War II, Dantzig and his coauthors generated an optimal tour through forty-nine cities—one in each of the contiguous states, as well as Washington, DC. Image from George Dantzig, D. Ray Fulkerson, and Selmer Johnson, “Solution of a Large-Scale Traveling Salesman Problem,” Operations Research, no. 2 (1954).

A 1962 advertising gimmick by Procter & Gamble hitched the TSP to a popular TV cop show—and offered $10,000 for the best itinerary for an assigned thirty-three-city tour. The prize money was eventually pocketed by Gerald Thompson, a mathematician at Carnegie Mellon, though not before he was obliged to draft a tie-breaking essay on the virtues of P&G’s soaps. Image courtesy William Cook.

The early 1960s saw the earliest intensive use of electronic computers in TSP research. The new computational power changed the kinds of solution strategies available. TSPs are solved by adopting a variety of tactics that narrow the domain of possible routes, or otherwise point out promising avenues. These approaches are often very beautiful (one of the most intuitive and elegant is a mathematical version of ant-swarming behavior, where best routes are amplified over time by means of a build-up of “pheromones”—a sequential weighting of routes that have proven productive in the course of millions of random walks). Richard Karp, shown at right here with colleagues at IBM, was a pioneer of what is known as “Branch and Bound” technique. Using it, he and Michael Held (at left) bested Dantzig et al’s forty-nine-city record by producing an optimized fifty-seven-city tour in 1964. Image courtesy William Cook.

In 1977, Martin Grötschel, focusing on a graphical technique known as “comb inequalities,” generated a then-stupefying 120-city optimized tour of West Germany. Image courtesy Martin Grötschel and Manfred Padberg.

The TSP has various practical applications. a prominent one is in the design of automated drilling, etching, and soldering routines used in the production of microchips. In the 1990s, William Cook, David Applegate, Robert Bixby, and Vasek Chvatal developed a powerful computer program known as Concorde (now available as an iPhone app) which can solve very large TSPs. Shown here is an 85,900-point tour that solves a chip-design optimization problem. Image courtesy William Cook.

The world as a TSP: a graphical representation of a tour of every point on the globe where the UN recognized human habitation in 2001. This image represents a solution within one tenth of a percent of the optimum. (It is a peculiar and important feature of the TSP that the length of optimal circuits can be calculated exactly—even if the actual route itself is not known; right answers are thus quickly and easily verified.) Work on this particular global data set has been more or less continuous across the last decade, and the current best routes are in the neighborhood of 7,514,000,000 meters. Image courtesy David Applegate.

Specifically the “P versus NP” problem. At stake is the issue of whether there exists a polynomial-time solution to all problems for which there is known to be a polynomial-time algorithm for solution verification. A finding in the affirmative (“P=NP”) would have significant implications for cryptography. Some have argued that the impact would be world-historic (an informed commentator recently opined in print that a proof of P=NP would “make the whole Internet look like a footnote in history”). For a general introduction to these matters, see Christos Papadimitriou, Computational Complexity (Boston: Addison-Wesley, 1994). The million-dollar Clay Prize is actually on offer for a solution to P versus NP, but a general polynomial-time algorithm for the TSP would amount to a proof that P=NP and thus bag the prize.
On the Handlungsreisende, see William J. Cook’s In Pursuit of the Traveling Salesman: Mathematics at the Limits of Computation (Princeton, NJ: Princeton University Press, 2012). Special thanks to Professor Cook for his generosity in sharing expertise and source material.

D. Graham Burnett is an editor of Cabinet.

If you’ve enjoyed the free articles that we offer on our site, please consider subscribing to our nonprofit magazine. You get twelve online issues and unlimited access to all our archives.